Drawing a Curvillinear Circle With Asymptote

Functions, Graphs, and Limits
- Intro
- Topics
- Limits
- Functions Are Your Friend
- Graphing and Visualizing Limits
- Piecewise Functions and Limits
- One-Sided Limits
- Limits via Tables
- Limits via Algebra
- All About Asymptotes
- Vertical Asymptotes
- Finding Vertical Asymptotes
- Vertical Asymptotes vs. Holes
- Limits at Infinity
- Natural Numbers
- Limits Approaching Cypher
- Estimating a Circumvolve
- The Cantor Set and Fractals
- Limits of Functions at Infinity
- Horizontal, Slant, and Curvilinear Asymptotes
- Horizontal Asymptoes
- Slant Asymptotes
- Curvilinear Asymptotes
- Finding Horizontal/ Slant/ Curvilinear Asymptotes
- How to Draw Rational Functions from Scratch
- Comparing Functions
- Power Functions vs. Polynomials
- Polynomials vs. Logarithmic Functions
- Manipulating Limits
- The Basic Backdrop
- Multiplication by a Constant
- Adding and Subtracting Limits
- Multiplying and Dividing Limits
- Powers and Roots of Limits
- In the Real World
- I Like Abstruse Stuff; Why Should I Intendance?
- How to Solve a Math Trouble
- Examples
- Exercises
- Quizzes
- Terms
- Handouts
- Best of the Spider web
- Table of Contents
At a Glance - How to Depict Rational Functions from Scratch
We now have plenty tools to draw some complicated functions from scratch. Now we know how graphing calculators exercise information technology, and why they require the energy of four triple-A'south.
When drawing a rational function f(x) from scratch, we demand to know a lot of information, which can be nicely grouped into iii big chunks.
- Nosotros need to know where f has vertical asymptotes and/or holes.
- We need to know the horizontal/slant/curvilinear asymptotes of f, if whatever.
- We need to know about values of f. We found where f is undefined when we found the vertical asymptotes and holes; at present we demand to know where f(ten) is 0, positive, and negative. We also want to know f(0), also called the y-intercept.
- Examples
- Exercises
Case 1
| Graph the function | |
| Go through the categories.
Taking this information, nosotros draw the graph: |
Example 2
| Graph the function | |
| f has a vertical asymptote at x = 0, and no holes. We can start cartoon: Since the degree of the numerator and denominator are the aforementioned, f has a horizontal asymptote at y = three: f is 0 when its numerator is 0 and its denominator is not. This occurs when The simply thing left is to find where f is negative and positive. When We now have enough information to go a rough sketch of the piece of f that lies to the left of the vertical asymptote at y = 0. When x > 0, the numerator and denominator are both positive and f is positive. Since f must approach its asymptotes, f looks like this: We didn't demand to worry most f(0) for this function, since f is undefined at 0. A number line is a useful tool for figuring out where a office is negative and positive, and we'll use this tool in i of the examples. Wherever f is 0 or undefined, its sign has the ability to change. Draw a number line and marker all the values of ten where f is 0 or undefined. From this, observe the sign of f in between those marked values. |
Example iii
| Graph the role | |
| Start we need to factor. There is no way to simplify this function; no terms volition cancel. Nosotros find no holes, but vertical asymptotes at 10 = -3 and x = -1: Since the caste of the numerator and degree of the denominator are the same, we have a horizontal asymptote at The function is 0 when the numerator is 0, which occurs at x = -2 and x = 1: Now nosotros demand to figure out where the function is negative and where it is positive, which we can do with a number line: Finding f(0): Nosotros can add together this point to the graph: We know some points of f, nosotros know where information technology is 0, negative, and positive, and nosotros know information technology must approach its asymptotes, and so f must look like this: We haven't explained how we know that f has the shape it has, and we won't get to that until we starting time talking about concavity. For at present, think near drawing the functions to make them "polish," similar MJ's criminal. Remember that intercepts are where a function crosses the axes. The y-intercept is f(0), if that exists. The x-intercepts are all values of x where the office is 0. |
Example 4
| Graph the office Label all asymptotes, intercepts, and holes. | |
| Kickoff we cistron: We take a vertical asymptote at x = -1 and a hole at (1,eight): We have no horizontal asymptote, merely since the degree of the numerator is one greater than the degree of the denominator we do have a slant asymptote, which nosotros can find via long segmentation: We have a slant asymptote at y = 410 + 8. We can draw that in too: Now we need function values. f is 0 when 10 = -3 and when 10 = 0: Finally, nosotros need to figure out where f is positive and negative: And now nosotros can fill in the motion picture: |
Exercise 1
Graph the role. Characterization all asymptotes, intercepts, and holes.
Answer

Vertical asymptote at x = 1, horizontal asymptote at y = 0. No intercepts.
Exercise 2
Graph the function. Label all asymptotes, intercepts, and holes.
Answer
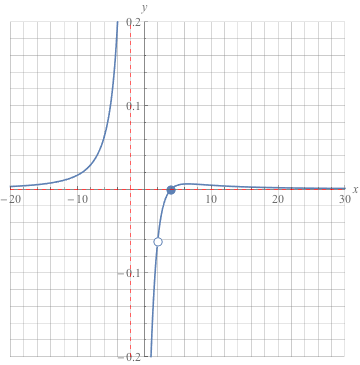
Vertical asymptote at x = -2, hole at (2, -0.0625), horizontal asymptote at y = 0. , and f(4) = 0.
, and f(4) = 0.
Exercise three
Graph the function. Characterization all asymptotes, intercepts, and holes.
Respond

Vertical asymptote at x = 3. Hole at (ane, -1.v). Horizontal asymptote at y = 1. and f is 0 when x = -2.
and f is 0 when x = -2.
Exercise four
Graph the function. Label all asymptotes, intercepts, and holes.
Answer
Vertical asymptotes at x = 1 and x = -1, horizontal asymptote at y = -1. f(0) = 0.

Do 5
Graph the function. Characterization all asymptotes, intercepts, and holes.
Reply

Pigsty at (-2,viii). Intercept at (0,0). Curvilinear asymptote at y = x 2. (This actually is the graph of 2ten 2, but with a hole at (-2, eight).
Source: https://www.shmoop.com/functions-graphs-limits/drawing-rational-functions-help.html

 .
.
 .
.

 .
. the numerator and denominator are both negative, therefore f is positive. When
the numerator and denominator are both negative, therefore f is positive. When  , the numerator is positive and the denominator is negative, so f is negative.
, the numerator is positive and the denominator is negative, so f is negative. 





 :
:

 :
:


 .
.










