Introduction

One of the major enhanced oil recovery (EOR) techniques that have been evaluated to be useful is chemical enhanced oil recovery (CEOR). CEOR involves injecting chemicals (such as alkaline, surfactant and polymers) to alter the fluid/fluid or rock/fluid interaction, thereby improving oil productivity (Gbadamosi et al. 2019). The technique witnessed major challenges since the mid-1950s of the last century. Recently, CEOR techniques undergo a revolution. Although the oil price dropped, it has been revived. This is mainly because of the advances in chemical formulation method, cheaper prices and advanced laboratory screening equipment (Abbas et al. 2017a; Agi et al. 2018; Hirasaki et al. 2008; Kamal 2015).

Recent developments of chemicals provided the industry with several new surfactants that can work under different conditions. Current interest nominated new types of surfactants such as viscoelastic surfactant (Bidhendi et al. 2018), gemini surfactants (Mondal et al. 2015; Pucciariello et al. 2004) and natural surfactants (Moslemizadeh et al. 2016). Most of the new generation of surfactants has not yet been tested in oilfield and still in the experimental stage. Despite the various types of surfactants, all categories share the same mechanism to mobilize the trapped oil. Surfactants are composed of two groups, specifically the hydrophilic head and the hydrophobic tail. The surfactant hydrophilic head attracts the water. On the other hand, the hydrophobic tail attracts oil. This attraction results in reducing the interfacial tension (IFT) between the two phases (oil and water) (Abbas et al. 2017c). In oil reservoirs, the IFT between the oil and water is between 29 mN/m and 40 mN/m. The surfactant can reduce the IFT to 10−3 and 10−4. Any IFT reduction will permit the residual trapped to flow more adequately through the pore (Kamal et al. 2017).

Although the new generation of surfactant is promising, several factors affecting the further implementation in oil fields remained blurred. Industry target is to achieve low surfactant concentration that can provide low IFT at harsh conditions. While this achievement seemed to be reached at the experiments, but it was not consistent in the literature (Puerto et al. 2018; ShamsiJazeyi et al. 2014; Wilson et al. 2019; Zdziennicka et al. 2012). Since the physical properties of the cores used among laboratory experiments are different, the validity range of the needed concentration goes under question (Abbas et al. 2019). In other words, there is no validation technique for the experiments. However, adopting the numerical simulation approach to generate matching with laboratory results is a common practice (Adepoju et al. 2017; Rai et al. 2015; Zhou et al. 2019).

There was a limitation of focus on surfactant flooding as a single flow in the recent literature. This is because most of the application included the addition of alkali or polymer or chase water to improve the total recovery. On a mechanistic level, Babadagli (2005) studied the continuous surfactant flooding on sandstone and limestone. The study used synthetic crude oil which exhibited moderate IFT in the presence of anionic surfactants (0.85 mN/m). The oil recovery was in the range of 50–60% in the sandstone. Another mechanistic study by Jamaloei and Kharrat (2010) examined the continuous surfactant flow that showed in 5 spot micromodel, the surfactant was able to reach 100% displacement efficiency. The results described that the surfactant was able to interconnect in the pore bodies. Majority of the published mechanisms emphasized on the applicability of the continuous surfactant flooding for wide range of oil types, reservoir condition and reservoir characteristics (Sofla et al. 2016; Wang et al. 2011). Yet, the continuous surfactant flooding of a single chemical was seemed expensive for the field practical implementation.

Experiments performed on a long vertical soil column with brine contained 17.5 g/L NaCl, while the main oil used in the study was n-C10. In this process, the anionic surfactant sodium dodecyl sulphate (SDS) was continuously injected. During the experiment, the surfactant was flushed after 63 pore volume (PV) which showed a continuous ability to solubilize the oil. The only remained ganglia was near the production outlet. The oil mobilized was due to capillary pressure gradients caused by the increase in the available surfactant. The study used modified code designed to predict the surfactant-oil movement based on fractional flow, where the fractional flow depends on the rate of the fluid flow in the porous media (Tsakiroglou et al. 2013). Lately, a numerical model was developed to predict the oil recovery of continuous surfactant flooding and the related sensitive parameters such as adsorption and physical properties. In general, the recovery factor was obtained on about 40–60% (Druetta and Picchioni 2020).

Despite the development of numerical and experimental matching techniques, carrying out numerous numbers of models for each experiment is not efficient. Accordingly, for optimization, sensitivity analysis and uncertainty evaluation, few approaches were suggested. Proxy models help to reduce the time required for full numerical modelling (Santoso et al. 2019). The proxy model basically merges the statistics and physics to aid the simulation and reservoir decision (Tanaka et al. 2020). Applying the proxy models generates a big number of data derived from the initial numerical simulation run at a grid level. The result of numerical simulation is used to train the new model. The new model honours the diffusivity equation and thus can mimic the numerical reservoir results to a good extent (Carreras et al. 2006).

One of statistical concepts used in proxy models is the response surface method (RSM) related by design of experiment (DoE). DoE is a set of sample points that are used to fit the regression models. For reservoir engineering models, it can be collected by petrophysical range, previous models, analogous field data or laboratory flooding results. The RSM is basically a mathematical form that describes a relation between the variables. The variables can be mathematically modelled either by linear or a quadratic function. The range of error in the developed mathematical equation can be minimized by a polynomial function and the least-squares methods (Liski et al. 2002).

In term of chemical flooding, few studies reported to adopt the RSM method. Ghadami et al. (2015) studied the parameters that affected the efficiency of alkaline-surfactant-polymer (ASP) flooding by RSM. The study revealed that the residual oil reduction, slug size and chemical concentration have the highest impact. Le Van and Chon (2016) used RSM for the optimization of enhanced heavy oil recovery by chemical flooding for economic purposes. The study focused on the impact of chemical concentration, slug size and pore volume injected on the net present value for the operation. Research found that the RSM was useful to minimize the number of options for the ASP implementation from an economic point of view. Moreover, RSM was recently used for optimizing the formulation of zwitterionic microemulsion to obtain an equation that can predict the concentration. The study found that additional surfactants concentration—above the critical micelle concentration—can increase the volume of microemulsion generated. In fact by the applied RSM, the equation showed a proportional relation between the surfactant concentration and the square of the concentration. The positive coefficients adhere to the increasing volume of microemulsion generated (Kumar et al. 2019). It is worthy to note that previous researches have focused only on ASP application and its related chemical properties.

This research focuses on the applicability of continuous surfactant flooding (CSF) in Bentiu reservoir. The study is limited to di-chain surfactant that was recently recommended (Abbas et al. 2019, b; Behrens 2013; Pucciariello et al. 2004). The study aims to relate the core's physical properties (porosity and permeability) and surfactant to the oil recovery and production. The developed steps consist of numerical run supported by a sensitivity study using Proxy Model/RSM. Adopting the current method helps shed light on the interrelation between the parameters and their effect on reservoir performance. This research designed an innovative solution to the lack of the cores taken from Bentiu reservoir in Sudan.

Methodology

Geological description

The Muglad Basin was explored by Chevron and partners in the early 1970s. The basin extends from the Republic of Sudan to the Republic of South Sudan as seen in Fig. 1a. The basin nature indicates it is an intra-continental rift basin. The formation process is labelled as right-lateral movement on the Central African shear zone at the Early Cretaceous. The basin marked two main productive sandstones which are Bentiu Formation and Darfur Group as seen in Fig. 1b.

Fig. 1
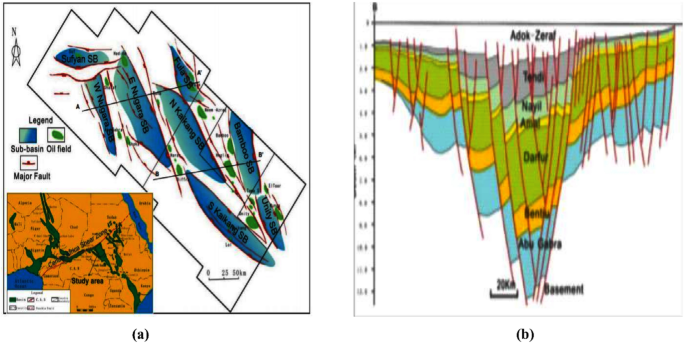
figure 1

a Structural units in the Muglad Basin, b structural cross sections across Muglad Basin (Arya 1986)

Full size image

Bentiu formation was deposited at the late Albian-Cenomanian. The interpretation of Bentiu deposition went through several phases. The first reported deposition showed alluvial and fluvial-floodplain environments. Currently, the advancement in understanding the geology indicated that the formation is by channel and braided river in nature.

Bentiu characteristic and properties

Bentiu reservoir is a sandstone formation. The sandstone is coarse- to medium-grained sandstones with pebbles, poorly sorted; lamination depends on flow regime and erosive contact. The core data have been collected from different locations targeting Bentiu at several depths. The total number of cores collected was thirty-six. The conventional core analysis (CCA) reported data for porosity and permeability are as seen in Table 1.

Table 1 Cores grouping and corresponding porosity and permeability

Full size table

In terms of porosity, several reports show a range from 4% to 32.20%. The pore interconnectivity varies from poor to very good, as seen in the thin section photomicrograph presented in Fig. 2a, b. These porosity values were affected by several diagenetic processes, which have either resulted in a decrease or an increase in reservoir quality. However, the targeted cores for this study have moderate porosity and moderate to high permeability as seen in Table 1. For the core permeability, the range of permeability shows a range between 200 mD and 6500 mD. The relation between cores porosity and permeability indicated high heterogeneity as seen in Fig. 3.

Fig. 2
figure 2

a Moderately sorted to well sorted; sub-rounded to sub-angular grains of monocrystalline quartz with significant quantities of polycrystalline quartz and indication of K-feldspar and trace amounts of heavy minerals enclosed in the quartz grains. Porosity is 21% with good pore interconnectivity. b Poorly sorted, sub-rounded to sub-angular grains of monocrystalline quartz with few amounts of polycrystalline quartz. Indication of K-feldspar, mica and heavy mineral grains. Porosity of 4.40% with poor pore interconnectivity

Full size image

Fig. 3
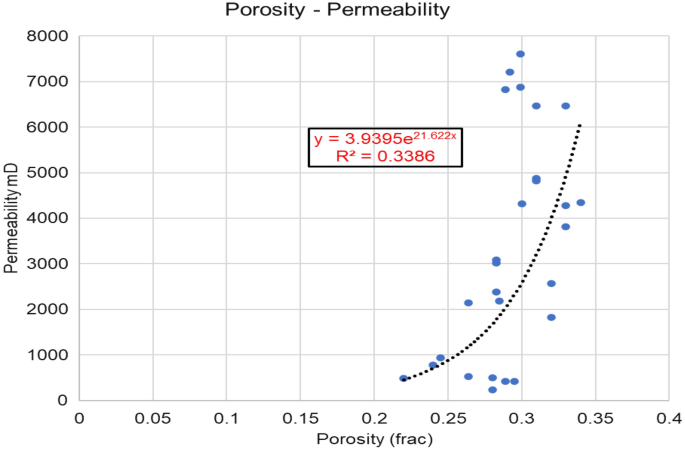
figure 3

Porosity permeability relation

Full size image

Relative permeability curve

The relative permeability curve was used based on the permeability. Each group have been assigned to a certain curve based on the average permeability.

Surfactant preparation and interfacial tension measurement

Aerosol-OT (sodium bis (2-ethylhexyl) sulfosuccinate, AOT) is a versatile anionic surfactant. The Aerosol-OT was purchased from Acros Organics BVBA (Geel, Belgium) at 96% purity. The chemical formula of Aerosol-OT is C20H37NaO7S with a molecular weight of 444.55 g/mol. The surfactant was prepared at different concentrations at the initial salinity of water formation in Bentiu reservoir. The water ion analysis is as seen in Table 2.

Table 2 Formation water report

Full size table

Easy Dyne Kruss Tensiometer was used to measure the interfacial tension between the oil and the surfactant. For each concentration, the reading was taken three times to ensure the IFT stability.

Simulation models

Since most of the commercial software provides similar basics of diffusivity equation solution, the computer modelling group software was selected for this purpose. For surfactant flooding, CMG-STARS was used to simulate the core runs. STARS proved to be useful in simulating laboratory scale and cores results (Abbas et al. 2020a; Rai et al. 2014). The core was modelled by assuming the cubic shape instead of cylindrical shape to simplify the initial flow difficulties. By using the BUILDER interface in CMG, the model was built with Cartesian coordinates and is divided into 15 blocks as seen in Fig. 4. The model initial input data are as provided in Table 3. The model was initialized at ambient conditions only to avoid the impact of the variation of the pressure and temperature in the reservoir at different locations. Due to the variation of each group porosity and permeability, the average values were calculated and used as input, as seen in Table 4, resulting in 5 main models. For the initial condition of relative permeability, it was generated from the available laboratory reports. The laboratory reports used the water–oil relative permeability unsteady-state method; the average value for relative permeability curve after grouping is as depicted in Fig. 5. To create a comparative study, the water flooding scenario was compared to the continuous surfactant flooding (CSF). The time-step taken was 5 min counted from the start point. The surfactant mole fraction used in the CSF was calculated via the software after using the critical micelle concentration and corresponding IFT obtained from the experiment. It is worthy to note that the production and injection constraints remained constant for all the models.

Fig. 4
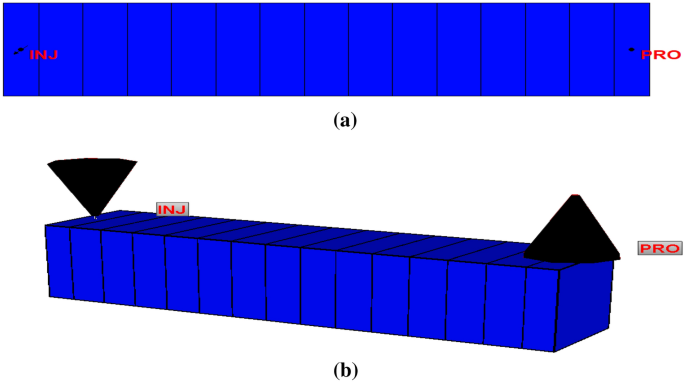
figure 4

a I–J view for core model, b 3D view for core model

Full size image

Table 3 Model initialization and input data

Full size table

Table 4 Average porosity and permeability

Full size table

Fig. 5
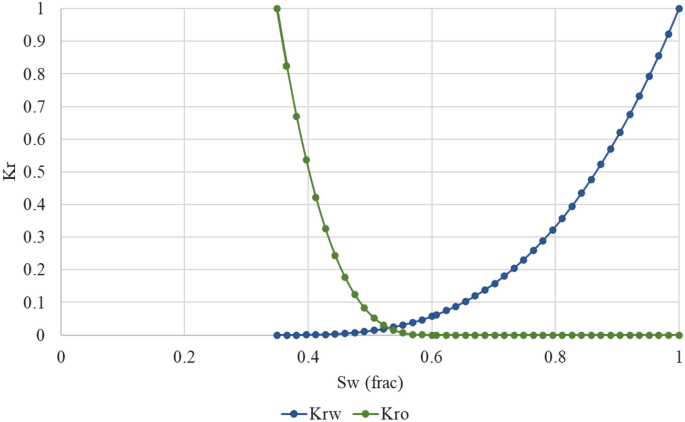
figure 5

Relative permeability curve

Full size image

Sensitivity study

Sensitivity analysis is a quantification to evaluate the effect of any parameters on the simulation results, which reduces the ineffective parameters. Reducing the ineffective parameters help in evaluating the potential of a field, which improves the representative of the model to mimic the subsurface. Several studies on experimental and simulation of chemical flooding in cores indicate that the most sensitive parameters are: chemical slug size, IFT reduction and chemical concentration (Alsofi et al. 2013). The slug size is not evaluated in the current study since the continuous surfactant flooding and water flooding consist of a similar pore volume injection. On the other hand, the relationship between the surfactant concentration and core physical properties significantly impacts the recovery factor and production in the field operation (Ghadami et al. 2015). However, this relationship needs investigation to reach a holistic vision for the reservoir. The workflow and sequence of the study are as seen in Fig. 6. Initially, the result obtained from CMG-STARS was selected for the original time series domain, followed by the selection of the three main properties under investigation (surfactant concentration, porosity and permeability). A uniform discrete with 10 intervals for each of the three properties was specified for each core. The two main objective functions are oil production and oil recovery factor (RF).

Fig. 6
figure 6

Study workflow

Full size image

Proxy model generation

Proxy model depends on the data set and algorithm used to generate the model. In order to achieve a robust valid model, it is essential to use a proper experimental design (Yang et al. 2007). From the literature, it is known that there is intense uncertainty related to the physical properties such as porosity and permeability. It is noted that both parameters affect the fluid dispersion and consequently the oil production. Accordingly, the oil recovery and production response are functions of the range of the deterministic uncertainty (Zabalza-Mezghani et al. 2004). In order to develop a representative experimental design, it is useful to fill the boundary between the deterministic discrete intervals. For some cases, LHS was found to provide an accurate sampling process compared to the random selection. This is because LHS provides a satisfying mean and variance and covers all the selected intervals of the sample (Wang 2003). Furthermore, considering the relation between the porosity and permeability brought attention to the possibility of using fractional factorial design. The fractional factorial is useful in understanding the factor interactions. By the use of this method, the relationship between porosity and permeability will be projected as well as the relationship between the concentration and the both parameters, if any. This method will allow the qualitative evaluation to be feasible (Voelkel 2005). Despite the efficiency of both method to represent the parameters interaction and output sensitivity, the main issue is the limited resources to evaluate the cores individually or to obtain more core from Bentiu formation. Therefore, by using some user input based on previous studies on the same area, the results will be helpful in general quality check of the model. This is basically an approximation to avoid unnecessary overestimation of the final output. During the pre-evaluation, it comes to the attention that the limited number of the cores might not reflect the complexity and heterogeneity of the reservoir. However, the hypothetical condition of allowing the model to run 100 samples might be a good reflection of the future evaluation. Therefore, the current study developed a combination of 100 samples using the three mentioned methods.

Results

IFT measurement results

Sudanese crude oil is typically medium dense crude oil. The IFT of the Sudanese crude versus water is 29 mN/m which is considerably higher than that expected for medium oils. This might be attributed to the nature of the crude which contains C7+ component as reported by previous studies (Tang et al. 2013). By increasing the surfactant concentration, the IFT reduced till there is no more reduction observed as seen in Fig. 7. The lowest IFT was noticed at a maximum concentration of 0.1 wt%.

Fig. 7
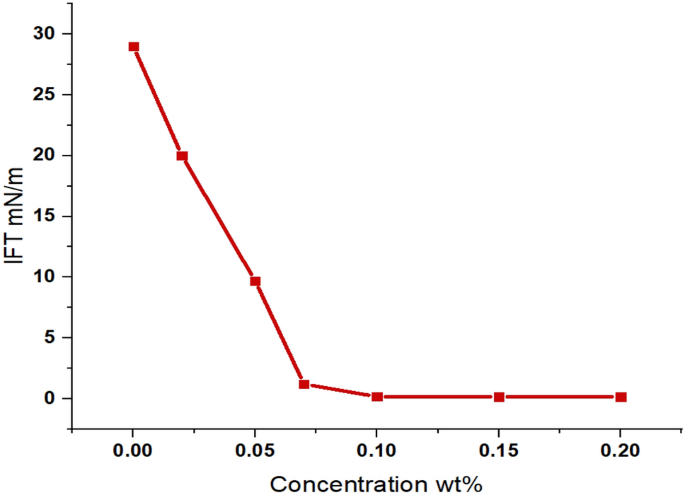
figure 7

Surfactant concentration versus IFT

Full size image

Further addition of the surfactant only resulted in a slight increase and fluctuation in the IFT. The reduction of IFT was around 93%, with a lowest value of 0.17 mN/m. The reduction shows 10−2 magnitude which is favoured for surfactant practice. Regardless, the surfactant performance was significantly viable. The observation justified by the ability of surfactants to adsorb on both crude and water interface (Ali 2011). Besides the surfactant ability to reduce the IFT, the salinity played a role in the reduction of IFT (Al-Sahhaf et al. 2007; Feng et al. 2018; Puerto et al. 2012). The presence of salts assists in altering the distribution of the surfactant molecules between the oil and water.

Simulation modelling results

Since the target of this study is to understand the maximum trapped oil production by CSF, the CSF is not followed by chase water. The initial surfactant concentration used of 0.1 wt% remained constant in all cases. Therefore, the water/surfactant was mainly injected as a single phase.

Base case scenario (Waterflooding)

By running the STARS Software, the water flooding capability was evaluated. The results revealed typical water flooding for all the factors as seen in Table 5. As illustrated in Table 5, the highest oil production was obtained in core 5, while oil production is lowest is in core 2. Since core 1 had the lowest porosity and permeability, it was expected it would have the lowest values for oil production and oil recovery. By looking at the oil recovery, we find that the oil recovery remained in the same range (44% oil recovery). Core 2 has the highest oil recovery factor which is approximately 44.67%. However, the difference is to consider insignificance (± 0.13%). In view of oil saturation, it remained in the range of 0.42. One of major issue that has been discussed for Bentiu reservoir is the high heterogeneity. This makes it very vital to understand the displacement efficiency for any flooding operation. In waterflooding, the displacement efficiency was approximately 44%, which is typical of displacement efficiency for waterflooding projects. However, since this is only a core application, it might need further investigation at more complex levels. Regardless, the oil saturation results had similar residual values. This may attribute to capillary pressure that trapped the oil (Abbas et al. 2017b; Xu et al. 2016). Since the study used grouped capillary pressure and relative permeabilities in core flooding, the results neutralized the impact of lithological vertical characteristics. It is worth noting that Bentiu reservoir in several mature oil fields was subjected to long waterflooding projects. The results of continuous water injection resulted in a drastic reduction in oil production. Several authors reported the negative impact of a traditional waterflooding scheme that has been applied (Zhao et al. 2010).

Table 5 Waterflooding main results

Full size table

Effect of CSF on oil recovery and production

The CSF showed increasing oil production in general compared to waterflooding. The highest oil production is for the core 5, while the lowest is in core 2. In Fig. 8, the results of oil production in response to the injected pore volume showed a variation in oil production at the beginning of the flood. This behaviour is attributed to the changes in the pressure across the core during flooding. As the initial core pressure was 101 Kpa, we found that at the time of injection, the pressure increased to 120–145 Kpa. The pressure increases because of the massive generation of oil. This behaviour has been observed in surfactant flooding. Ultimately, the current case is representing medium oil which makes the generation of bulk oil as expected. A similar observation has been noticed in previous work by Hosseini et al. (2019).

Fig. 8
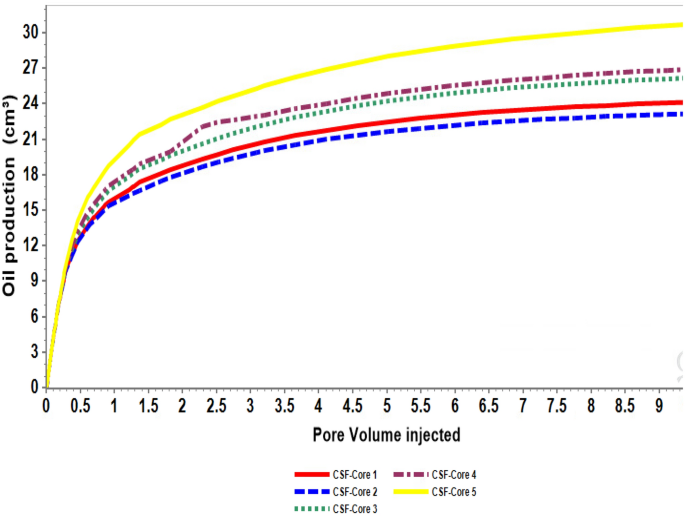
figure 8

Oil production by CSF

Full size image

The recovery factor trend, as seen in Fig. 9, showed very close results at the end of the process. The difference between the recovery was in the range of 1.5% for the low range of porosity and permeability as in core 1, 2. For the higher range as in core 5 and 4, the difference was noticed to be approximately 3%. This additional recovery attributes to the size of the pores and the surfactant accessibility to the oil. Figure 10 shows that the remaining oil saturation distribution changes as a function of the distance from the injection point. In addition, it can be noticed that the remaining oil is changed based on the core characteristic. However, at the end of the flooding, the average residual saturation is semi-equivalent for all the cores as seen in Table 6. As the displacement efficiency might explain the general behaviour of CSF flow which was highly notable by 30% compared to the traditional water flooding, the results does not essentially describe the flow in each grid as proved by saturation changes in Fig. 10. By comparing Table 5 and 6, it is clear that the results of each aspect improved. The findings of these models are slightly different in comparison with the previous studies by Abbas, et al. (2018). The significant difference could be noticed in the range of oil recovery factor at the high range of porosity and permeability (core 4 and 5). The current study showed a possible addition of 4%, moreover, in comparison with the results obtained by Ali et al. (2011), for oil production. It seems the current results are promising. The main reason behind the improvement in oil production is because of the nature of Aerosol-OT. Accordingly, the surfactant reduced the IFT to a lower degree.

Fig. 9
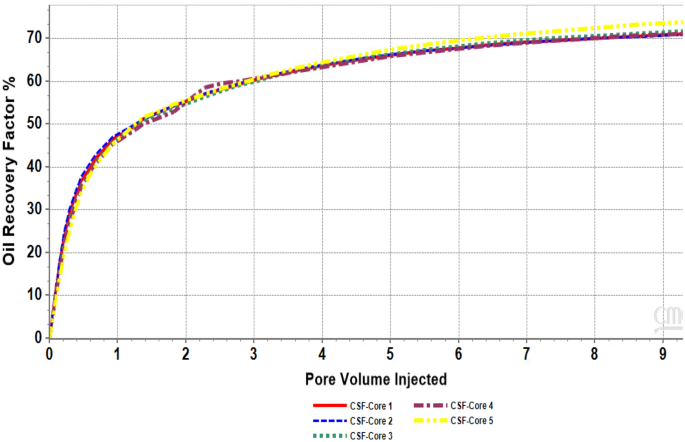
figure 9

Oil recovery by CSF

Full size image

Fig. 10
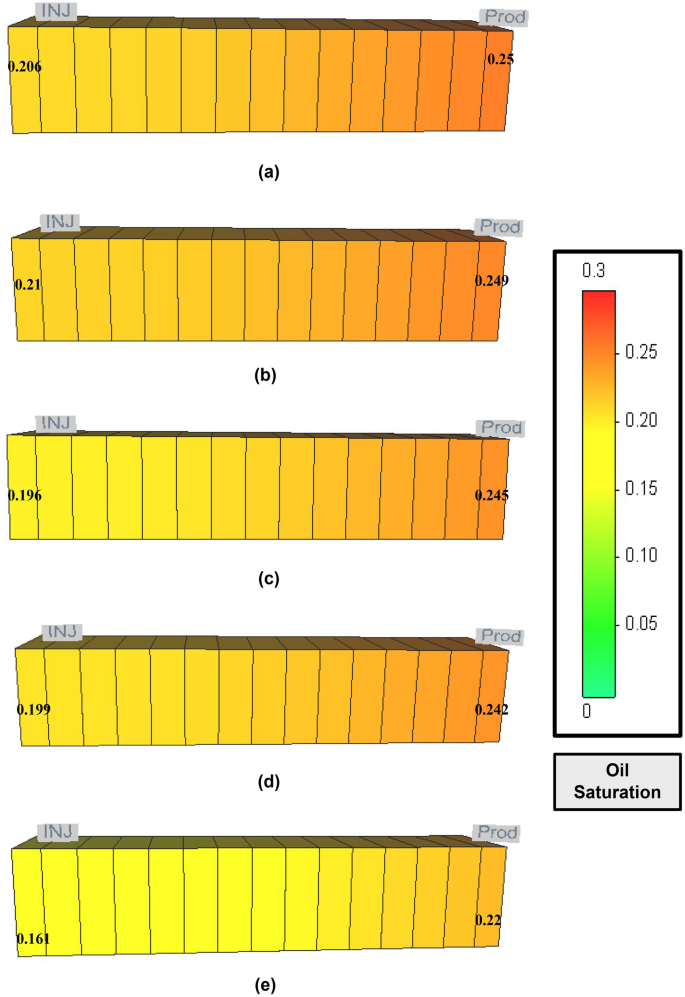
figure 10

The changes of oil saturation at the end of the injection a core 1, b core 2, c core 3, d core 4 and e core 5

Full size image

Table 6 Summary of CSF main results

Full size table

Sensitivity study by proxy model

Generally, the proxy models are designed to facilitate the history matching between the numerical solution and field crucial factors. The proxy model provides some modification for the targeted outputs without the need of remodelling each case singularly. In this context, sensitivity analysis is intended to describe the variance in oil recovery, oil production and residual oil saturation as function of surfactant concentration, porosity and permeability. This most straightforward approach will lead to understanding the variables importance and their effect on result alteration. For Bentiu reservoir case, the proxy model is generated to compensate for the lack of core taken and to highlight the optimal condition for future implementation.

Oil production by proxy model

Oil production is important in the decision making of oil and gas projects. Practically, the analysis of physical systems should strictly answer the project expectation to a sufficient confident degree. For the generated CSF proxy model, as seen in Fig. 11, the trained model indicates good fitting. The regression squared coefficient R 2 is 0.99. This implies with the current available data that the sensitivity study is reliable. The results in Fig. 12 show that the minimum oil production is 11 cm3 and the highest is 40 cm3. This range is considerably significant. By considering the main purpose of the sensitivity study, we can find that the most influential parameter that affects oil production is the porosity (Ø). The model found that there is insignificant impact of permeability (K) on oil production at the core level. For the surfactant concentration (C s), it shows a negative impact on oil production when the initial concentration is reduced. To confirm the modelled equation, the standard deviations of 1.119E10−7 and 1.14E10−7 were found for porosity and surfactant concentration, respectively. The standard deviation indicates a good degree of confidence for the given equation as illustrated in Fig. 11. Noting that the equation is obtained for oil production in m3 unit, the most important consideration for the equation is that the standard deviation and the regression coefficient error will be escalated in field level because of the higher complexity factors of interaction and heterogeneity.

Fig. 11
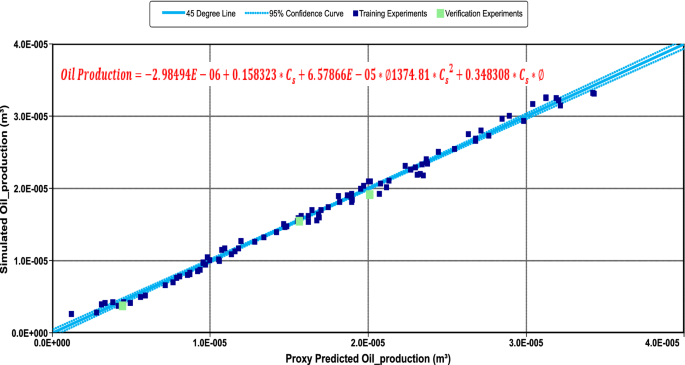
figure 11

Oil production fitting and proxy models equation

Full size image

Fig. 12
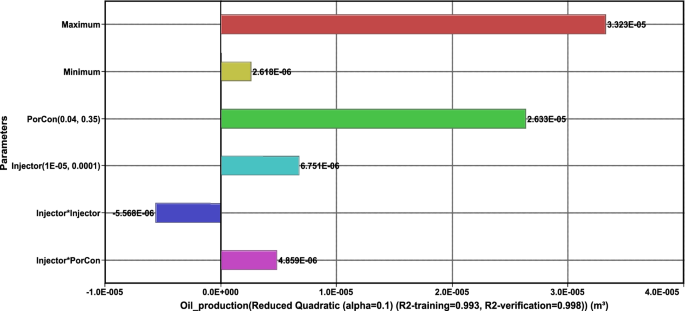
figure 12

Oil production values indication

Full size image

The results in Fig. 12 depict that the core is a simplification of the expected interaction between the factors and the observants during the flow. The interaction between oil production and porosity can be explained physically by the concept of larger pore capacity. The large pores contain a substantial amount of oil, which significantly contributes to the total production. The presence of surfactant has less effect on oil production since its primary purpose is to reduce the IFT and, consequently, the capillary pressure, which is less significant in large pores. Moreover, the current model assumed 12% of the experiments to be in an unfavourable condition. The assumptions are made to compensate for the expected worse scenario such as low porosity out of the cut-off limit or if the surfactant loss by the adsorption or any practical possible errors. Therefore, the current interaction can be used for qualitative purposes and to less extent to the quantitative purposes. It is worth noting that the unfavourable condition can be avoided by thorough optimization before the pilot test. Despite the confidence in the interaction level, it remains significant to define the range by the means of probability. Therefore, the probability distribution is presented by Monte Carlo in Fig. 13. Oil production probability sheds a light on the CSF application. For oil production in Bentiu-CSF, the results explain simply as P50 is somehow the most likely probability to occur and equivalent to an average value that most reservoir engineer practitioners look for. A less likely value of (P90) also could be used as an optimistic case condition in reservoir engineering context, although the (P10) is inversely to (P90). Focusing on (P50), it confirms around 17 cm3 for oil production. The results are less than what have been observed at the simulation runs. However, the optimistic value which is the lowest to occur (P90) shows 28 cm3 which is similar to the results in Table 5. This is explained by the numerical model initial input data without considering the lower concentrations. Additionally, for the optimist case (P90), the variation in the results falls in line with the accuracy of the model since most of the available cores were taken from good productive zones. By such implementation of sensitivity analysis in cores, the results solidify the numerical simulation results.

Fig. 13
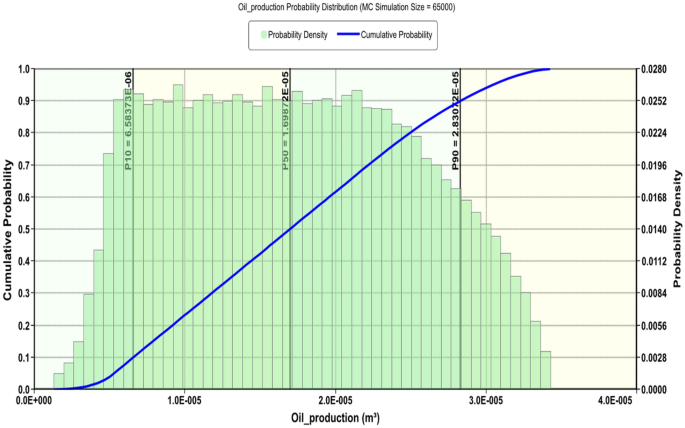
figure 13

Monte Carlo probability distribution for oil production

Full size image

Oil recovery by proxy model

After the model was trained, the regression squared coefficient R 2 for oil recovery factor was 0.95. As Fig. 14 indicates, the fitting equation was affected by lower case set of experiments. By analysing the oil recovery results, the oil recovery was sensitive to all factors. The obtained equation has a standard deviation of 2.4, and all parameters at the normalized fit had the standard deviation of (0.2–0.4), while the variables seem to be in a satisfactory range.

Fig. 14
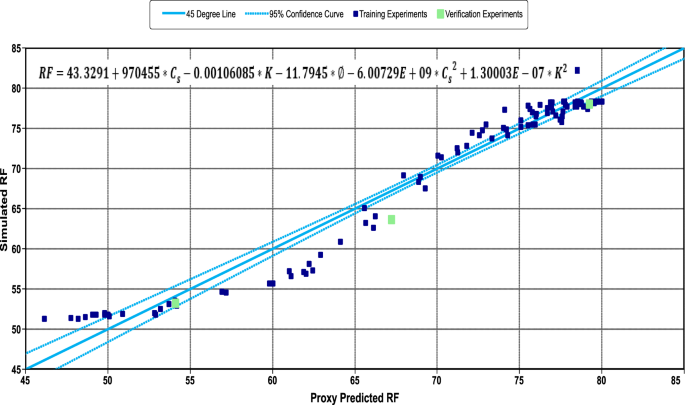
figure 14

Oil recovery factor fitting and proxy models equation

Full size image

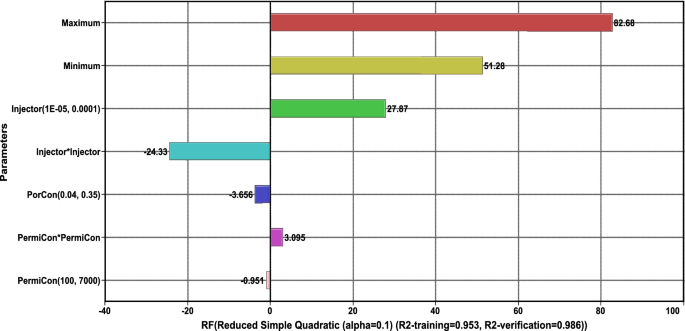
The parameter indication in Fig. 15 shows the oil recovery was the highest of 82% and the lowest of 52%. The recovery result confirms the applicability of the CSF even at the worst flow conditions, and all the results exceeded what was obtained by the waterflooding. The current findings seem to follow the expected range of the additional oil recovery by surfactants (Kamal et al. 2017; Raffa et al. 2016).

Fig. 15
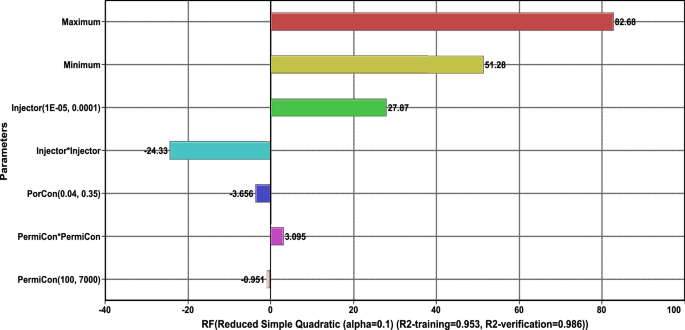
figure 15

Oil recovery factor values indication

Full size image

Moreover, for such very basic homogeneous model, these indications significantly prove the interrelation between the factors. Although the most influential factor for oil production was porosity, the surfactant concentration indicated the highest ranked for oil recovery. The surfactant concentration contributed 98% to the oil recovery changes. The interpretation of the shift is relevant to the fact that oil recovery is a fraction of production out of the total OOIP. Thus, the presence of surfactant assesses the release of the oil and reduces the residual oil quantity. The probability distribution of oil recovery presented in Fig. 16 showed that the most likely case (P50) is 74%, while the lowest (P10) is 55%. The fact that the reduction of the used surfactant concentration—since it is the most influence—is yet able to add additional recovery is very promising. The CSF proxy mode gives such assurance to the range determined in Table 5.

Fig. 16
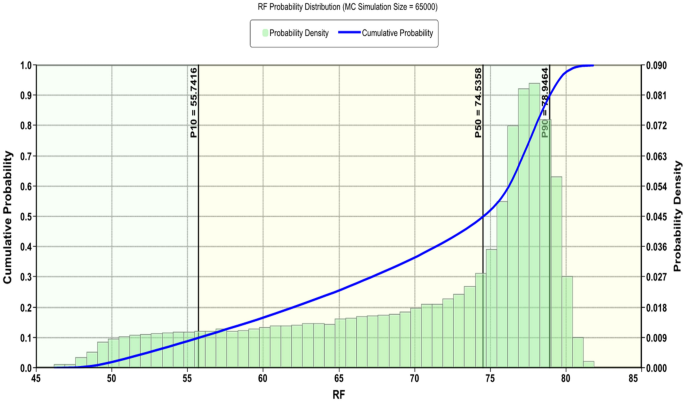
figure 16

Monte Carlo probability distribution for oil recovery

Full size image

Residual oil saturation by proxy model

In Fig. 17, the fitting equation of the residual oil saturation showed R 2 of 0.95. The fitting result indicates that the training of the model is representative. The residual oil saturation is dominantly affected by the available surfactant concentration. The trained model has standard error of 0.0018, and for each parameter, standard deviation is approximately 0.0025. By looking to the maximum and minimum of the residual saturation in Fig. 18, it can be seen that the CSF model can reduce the residual to 0.19. This value is lower than what has been attained by waterflooding by 58%. When the CSF was not in favour of the flow condition, the residual oil saturation was maximized by 5% compared to CSF numerical runs. Despite the addition in the residual, it is still lower than what has been found during the waterflooding by 16%. The indication of the parameters highlights the strong relation between the surfactant concentration and the residual oil saturation. In Fig. 19, the Monte Carlo results depicts that the likely case (P50) is approximately 0.2. This value is lower than the CSF numerical. It is because the current values were affected significantly by the low limit in the experiment design. Figure 19 shows a huge shift towards the optimistic case (P10) with the fact that the residual oil saturation may be reached to 0.15. In other words, the CSF might be significantly useful even at a low surfactant concentration, porosity and permeability. The current result is a compatible view of what obtained earlier by (Abbas et al. 2020b; Pucciariello et al. 2004) for the cases when surfactant diminished to lower value due to adsorption and surfactant loss in the porous media.

Fig. 17
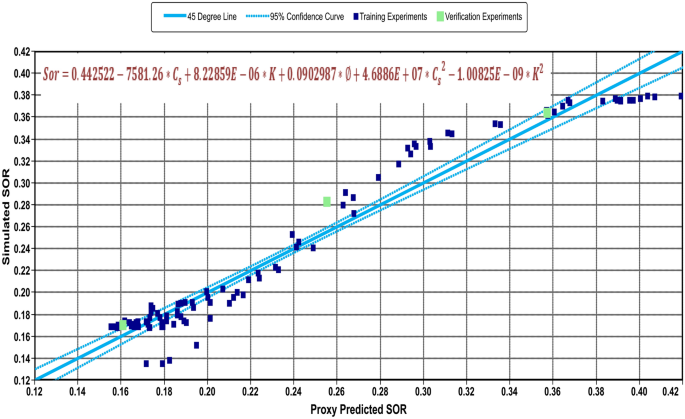
figure 17

Oil saturation fitting and proxy models equation

Full size image

Fig. 18
figure 18

Oil saturation values indication

Full size image

Fig. 19
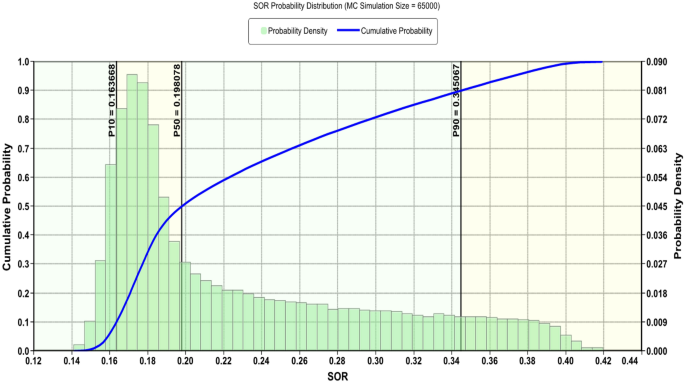
figure 19

Monte Carlo probability distribution for oil saturation

Full size image

Conclusion

This paper aimed to investigate the possibility of using CSF in Bentiu formation. The study grouped wide range of available cores from different fields. In order to get the utmost expectation about the oil production and recovery factor, the initial runs were validated by the proxy models using RSM.

The following findings could be concluded from the results:

  1. 1.

    During the numerical simulation, the use of CSF was able to improve the oil recovery by 20–30% compared to traditional water flooding. Between the available low range of cores, the difference in recovery was only 1.5% which increased significantly to 3% in range 4 and 5.

  2. 2.

    The sensitivity analysis obtained by the combination of LHS, factorial design and user definition provided a suitable fitting equation with R 2 of 0.95. The reliability of the model reached stable range after 100 experimental runs.

  3. 3.

    The expected oil production for the numerical simulation is in range of 23–31 cm3. This range shifted to be 11–40 cm3 in the proxy model. This is mainly because of the impact of surfactant concentration reduction and the porosity effect.

  4. 4.

    The generated proxy model showed a variation range of oil recovery in which the highest value was 85% and the lowest was 55%. The improvement in recovery is around 15%-40 compared to the water flooding. The result confirmed the effect of additional surfactant—even in low concentration—positive impact on the recovery

  5. 5.

    The residual oil saturation lowered by 58% in comparison with waterflooding. The average of residual oil saturation reached 0.2 which complies with the range of the numerical simulation

  6. 6.

    The complexity of interrelation between the factors was differ across the observant. The observation relates the oil production sensitivity to porosity and surfactant concentration, while the oil recovery and residual saturation showed more complexity in the equation and strong impact of permeability.

  7. 7.

    The current finding is subjected to iteration in oil field when more parameters involved in the overall performance of CSF. However, it is able to provide an expected range for the results with the aid of the proxy model.

  8. 8.

    For further applying the CSF in Bentiu formation, we find the possibility of unlocking the formation potential which requires further modelling and experimental prior to the application.